Projet d'Algorithmique Avancee: Outil de Recherche de Sous-mots

Licence Informatique 1999-2000, Université de Marne la Vallée

Daniele Raffo draffo@ken.univ-mlv.fr

mars-avril 2000

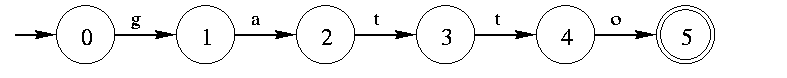
Source du programme (sousmot.c, 30623 bytes)
Licence Publique Générale GNU
Spécifications du projet (en Postscript, 52442 bytes)
Exemple du fichier d'automate (automate1)

SPÉCIFICATIONS TECHNIQUES

Le programme (environ 1000 lignes de code, 30623 bytes) a été écrit en ANSI C et compilé avec le compilateur GNU gcc. Il a été testé sous environnement UNIX sur machines 9000/755 HP-UX B.10.20 E (ken.univ-mlv.fr) et sun4u SunOS Solaris 5.6.
Le rapport a été rédigé en HTML 4.0 et les images ont été dessinées avec Xfig 3.2.
Pour compiler la source, taper la commande gcc sousmot.c -o sousmot. Pour exécuter le programme, taper ensuite sousmot (avec les arguments éventuels ci-dessous décrits).
Ce programme est sous la Licence Publique Générale GNU publiée par la Free Software Foundation.

PROGRAMME

UTILISATION DU PROGRAMME

Le programme peut être utilisé soit en mode interactif, soit en lui passant des arguments sur ligne de commande.

sousmot
Présente un menu permettant de tester les différentes fonctionnalités du programme.
En appuyant sur 1 on peut lire un fichier d'automate en l'affichant sur l'écran.
En appuyant sur 2 on peut vérifier l'équivalence de deux AFD (automates finis déterministes) complets, le programme demandera le noms des deux fichiers et affichera la réponse.
En appuyant sur 3 on crée un AFD complet qui reconnaît tous les sous-mots d'un mot tapé. On peut choisir si on veut afficher l'automate sur l'écran ou le mémoriser sur un fichier.
En appuyant sur 4 le programme engendre la liste de tous les sous-mots d'un mot donné. La liste sera montré à l'écran ou écrite sur disque, selon le choix.
En appuyant sur 5 le programme permet de calculer la liste de tous les sous-mots qui distinguent deux mots donnés. La liste sera montré à l'écran ou écrite sur disque, selon le choix.
Appuyer sur X pour sortir du programme.

sousmot -x fichier
Affiche sur la sortie standard l'automate décrit sur le fichier.

sousmot -e fichier1 fichier2
Teste l'équivalence des deux automates décrits dans les fichiers fichier1 et fichier2. Le code de retour (exit) 0 indique deux automates équivalents et le code de retour 1 indique deux automates non équivalents.

sousmot -s mot
Affiche sur la sortie standard tous les sous-mots du mot.

sousmot -s mot reference
Idem, mais la liste est placée dans le fichier reference.

sousmot -m mot1 mot2
Affiche sur la sortie standard la liste des plus petits sous-mots qui séparent mot1 et mot2.

sousmot -m mot1 mot2 reference
Idem, mais la liste est placée dans le fichier reference.

sousmot -h (ou n'importe quel autre format de paramètres non compris parmi ceux dessus)
Montre un écran d'aide avec ces informations.

STRUCTURE DE DONNÉES UTILISÉE POUR L'AUTOMATE

La structure de données utilisée pour stocker l'automate est une struct, contenant un array tridimensionnel table[][][] et un array monodimensionnel status[].
table est la table des transitions de l'automate. Le premier indice est le numéro de l'état, le deuxième l'étiquette de la transition, identifiée par son code ASCII; le troisième index sert, dans un AFND (automate fini non déterministe), à distinguer les éléments dans la suite des états d'arrivée (la fin de la suite est signalé par une valeur -1). Les éléments inexistants sont marqués avec -1. Donc, table[x][y][0]=z signifie que depuis l'état x, en lisant y, on va dans l'état z si z diffèrent de -1, et il n'y a pas de transition si z=-1. Ainsi si depuis l'état 7 on peut lire 'a' en allant dans l'état 5, on aura table[7][97][0]=5(97 est le code ASCII de 'a'). Si depuis l'état 7 on ne peut pas lire des 'a', on aura table[7][97][0]=-1. Si depuis l'état 7 on peut lire des 'a' en allant soit dans 8, soit dans 9 (c'est le cas d'un AFND), on aura table[7][97][0]=8, table[7][97][1]=9 et table[7][97][2]=-1. Pour un AFD, le troisième index sera inutilisé et toujours fixé à 0.
status mémorise les caractéristiques des états de l'automate: 1 si état initial, 2 si état terminal, 3 si état initial et terminal en même temps, 0 si état ni initial ni terminal. Les éléments non utilisés sont marqués avec -1. Ainsi si l'état 7 est terminal, status[7]=2.

Ma structure n'est ainsi pas limité au type d'automate demandé dans les spécification du projet, mais peut aussi bien contenir un AFD ou un AFND, complet ou pas. Les fonctions de lecture depuis fichier, affichage et initialisation peuvent opèrer sur de tels automates génériques. Cependant, en ce qui concerne le test d'équivalence et les opérations sur sous-mots, on se limite aux AFD complets qui sont nécessaires aux algorithmes (j'ai écrit une fonction qui contrôle l'aspect complet ou non de l'automate). Dans le cas du test d'équivalence, les AFND sont transformés en AFD en considérant seulement la première transition pour chaque lettre, selon l'ordre dans lequel elles sont écrites dans le fichier d'automate.
Les étiquettes des transitions peuvent être n'importe quel caractère ASCII 7 bit. Pendant toute opération sur un automate, la lecture des étiquettes des transitions sera effectuée en ordre ASCIIbetique. Des telles étiquettes sont identifiées par leur code ASCII, au moment de l'affichage ou de l'écriture sur disque de l'automate il sera fait un cast à char.

Cette structure de données a été choisie parce qu'elle est aisément lisible, étant basée directement sur un modèle graphique (un tableau) utilisé dans le travail sur les automates. Même si elle a le défaut d'allouer une considérable quantité de mémoire quelque soit la dimension de l'automate, les opérations sur ce modèle sont beaucoup plus simples et compréhensibles que dans un modèle fondé sur une liste chaînée (ma premiére hypothèse).
Le passage en argument de cette structure aux fonctions est toujours effectué par adresse, pour des raisons de mémoire; cela permet en plus de laisser libre le return pour le passage d'autres valeurs, car la structure est modifiée directement dans la fonction. Pour empêcher toute modification involontaire par les fonctions qui ne devraient pas écrire sur les données, elle est déclarée, le cas échéant, const dans les prototypes.

FONCTIONS

main() passe le contrôle à main_interactif() ou main_ligne_de_commande(), selon que l'exécutable soit appelé sans arguments ou avec.

output_sur_ecran() demande à l'utilisateur s'il veut que l'output (automate ou liste de sous-mots) soit à l'écran ou sur fichier.

La fonction init_automate() initialise le modèle d'automate, en assignant à tous les éléments de table et de status la valeur -1. (La valeur 0 serait ambiguë car il pourrait bien indiquer l'état 0 aussi).

La fonction lit_fichier() lit un fichier dans lequel est décrit un automate selon le format indiqué dans les spécifications du projet, et le stocke dans le modèle d'automate passé en paramètre. La fonction contrôle toujours le premier emplacement libre dans le modèle: si ce dernier contient déjà un automate, le nouvel automate y est mémorisé après. Cette implémentation rend plus facile le test d'équivalence.
Un système de contrôle des malformations (fichier d'automate qui ne respecte pas le format) y est inclus.

ecrit_automate() prends en argument un pointeur à fichier et une structure d'automate. Si le pointeur à fichier définit un fichier sur disque, elle y écrit l'automate mémorisé dans le modèle, selon le format indiqué dans les spécifications du projet. Par contre, s'il pointe à la sortie standard (l'écran par défaut) elle y affiche l'automate dans un format plus aisément lisible par les humains. Les états initiaux et terminaux sont indiqués.

La gestion des erreurs (dépassement des dimensions autorisées pour les données, malformation des fichiers d'automate, erreurs de lecture/écriture sur disque, tentative de faire tourner le test d'équivalence sur des automates non complets ou qui ont un différent langage des étiquettes) est faite au moyen de la fonction error(). Elle reçoit en paramètre, et affiche sur le standard error, des informations sur l'erreur qui s'est produit, et gère la sortie du programme avec code de retour diffèrent selon l'erreur.

Les autres fonctions sont décrites plus en détail dans les sections spécifiques de ce rapport.

SIGNIFICATION DES MACRO

MAX_ETATS est le nombre maximum d'états qu'un automate peut avoir.
MAX_ALPHA est le nombre de différents étiquettes existantes, et correspond à tous les différents caractères (0-127) du code ASCII 7 bit.
MAX_TRANS est le nombre maximum de transitions ayants la même étiquette, depuis un même état. Si on change cette valeur à 1, le modèle ne pourra que mémoriser des AFD.
MAX_L_MOT est la longueur maximale d'un mot à traiter. Défini comme MAX_ETATS-2, car un AFD complet reconnaissant les sous-mots d'un mot de longueur l nécessite l+2 états (voir dessous).
DIM_LISTE est la dimension d'une liste qui doit mémoriser un groupe de sous-mots de la même longueur.

DIVERS

Pour le deboguage du programme, j'avais utilisé à l'intérieur des morceaux de code qui affichaient (tracing) les valeurs de certaines variables dans des points cruciaux de l'exécution. Ces traceurs sont identifiés par les instructions if (TRACEON) { ... } .
J'ai décidé de laisser ces morceaux à leur place dans la version définitive, car ils peuvent être d'une grande aide pour la compréhension des algorithmes. Pour réactiver le tracing changer la valeur de la macro TRACEON du FALSE en TRUE.

TEST D'ÉQUIVALENCE DE DEUX AUTOMATES

Dans cette partie on vérifie si deux AFD complets sont équivalents, c'est-à-dire s'ils reconnaissent le même langage.

ALGORITHME

Je me suis servi de l'algorithme récursif canonique, qui utilise la notion de classe d'un état.
Une fonction equiv() reçoit en paramètre deux états e1 et e2. Elle vérifie d'abord s'ils sont tous les deux terminaux ou non terminaux: si c'est pas le cas, les deux automates ne sont pas équivalents et on sort de l'algorithme. Sinon, si e1 et e2 appartiennent à des classes différentes, on fait l'union des classes de e1 et e2 et on reappelle equiv() pour tous les couples d'états où on arrive en lisant la même lettre depuis e1 et depuis e2.
Si l'algorithme se termine sans que se produise la condition de sortie qu'on vient de décrire, les deux automates reconnaissent le même langage.
Le premier appel de la fonction equiv() est effectué en lui passant les états initiaux des deux automates.

La complexité est presque linéaire: O(card A x n x alpha(n)), où A est l'alphabet, n le nombre d'états et alpha la fonction d'union des classes (à considérer quasiment comme une constante multiplicative).

IMPLÉMENTATION

Elle est effectuée au moyen de la fonction equiv_automate(), qui crée un modèle d'automate atest accueillant les deux automates à tester, mémorisés dans les fichiers afile1 et afile2. Les deux automates sont mémorisés l'un après l'autre dans le même modèle (voici pourquoi la dimension du premier indice de table est définie comme MAX_ETATS*2). Ceci a l'effet de renuméroter automatiquement les états du premier automate et de rendre plus faciles les opérations.
La condition de sortie est indiquée par le changement du variable globale equivhalt. J'ai utilisé une variable globale pour éviter des situations compliquées dues à l'utilisation du return dans des appels récursifs.

REMARQUE

Qu'est-ce que c'est un AFD complet? Imaginons que depuis tous les états on ait les transitions avec les étiquettes a, b, c et d; selon l'alphabet {a, b, c, d} cet automate est complet; selon l'ensemble des caractères ASCII (utilisé dans mon projet), il ne l'est pas. Ça serait pénible de considérer complet seulement un automate qui a toutes les 128 transitions de l'alphabet ASCII, car il seront presque toutes vers l'état poubelle. Pour ça, j'ai écrit une fonction est_complet() qui contrôle que chaque état ait toutes les transitions, sur les mêmes lettres, de l'état 0 (mais on pourrait prendre un état quelconque au lieu de 0).

Pour ce qui concerne le test d'équivalence de deux automates, il faudra en plus vérifier que l'alphabet soit le même. (Sans cette vérification, le programme évaluerait faussement comme TRUE l'equivalence des automates des sous-mots des mots gatto et gattone). Cela est fait en appelant est_complet() pour le premier automate, ensuite pour le deuxième, enfin pour la structure où ces deux automates sont mémorisés l'un après l'autre: l'appel de est_complet() sur l'ensemble des deux automates complets donnerait la proposition FALSE si le deux automates (que nous avons déjà vérifié être complets) ne sont pas sur le même alphabet.

CONSTRUCTION DE L'AUTOMATE DES SOUS-MOTS

THEORIE

Etant donné un mot de longueur n, l'automate le plus simple qui reconnait ce mot est composé par n+1 etats (on les numérotera de 0 à n), parmi lesquels l'unique état initial est le premier et l'unique état terminal est le dernier, liés par des flèches étiquetés dans l'ordre des lettres du mot.
Voici l'automate du mot gatto:

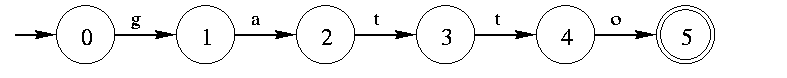
Un automate qui reconnait tous les sous-mots de gatto peut étre aisement obtenu par cet automate en ajoutant des epsilon-transitions entre tous les états adjacents:

On appellera M un tel automate, et on va se baser sur cet automate pour la construction d'un AFD complet equivalent qu'on nommera M'.
Soit q un etat de M. Ce type d'automate particulier a des proprietés interessantes: remarquons d'abord que e-clot(q)={q, q+1, q+2, ... , n-1, n}; donc si q1<q2, e-clot(q2) est contenue dans e-clot(q1) et par conséquence e-clot(q1) union e-clot(q2)=e-clot(min(q1, q2)). (1)
Il y a donc une bijection entre les états et leur epsilon-cloture.

ALGORITHME

L'automate M' aura n+2 états (les états de M, plus l'état poubelle), numérotes de 0 à n+1, où q'=e-clot(q) et q' terminal (car tous les q' contiennent le dernier état de M) pour 0<=q'<=n (c'est à dire, pour tous les états sauf la poubelle n+1). On pourra travailler sur les états de M', sans se soucier des epsilon-clotures, en se rappelant de la proprieté (1).

L'algorithme trouvé est derivé de l'algorithme canonique pour la determinisation des automates avec epsilon-transitions:
- Ecrire la table des transitions de M', avec les états dans les lignes et les lettres du mot dans les colonnes, dans l'ordre, en assignant les états à la table selon le critére: M'(i, j) = j+1 si j>=i, n+1 sinon (i et j demarrent de 0);
- Fusionner les colonnes correspondants à une meme lettre, en gardant pour chaque ligne la valeur la plus petite.

La première étape est déduite simplement de l'observation de M et de ses epsilon-transitions.
La deuxieme étape correspond à la fusion des epsilon-clotures et est une application de la proprieté (1). L'état poubelle ne gêne pas le déroulement de l'algorithme car il est l'état avec le numéro le plus grand.

La complexité de l'algorithme est O(n³).

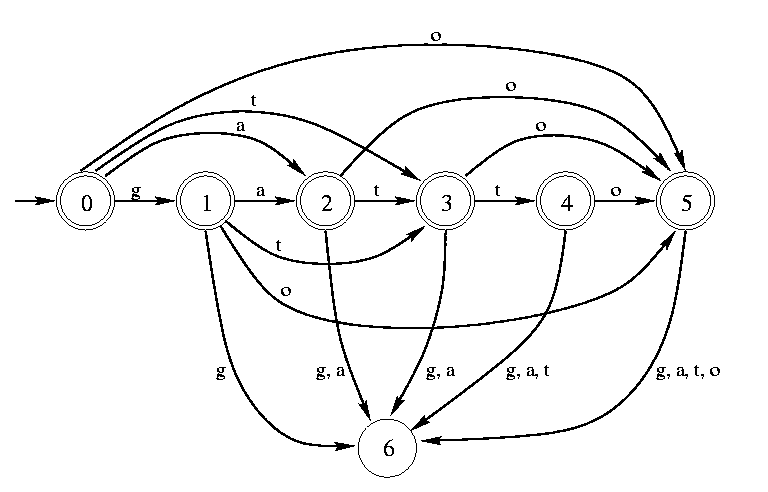
Ci-dessous est montrée la table des transitions, après la première et la deuxieme étape, de l'automate M', et l'automate lui-même.

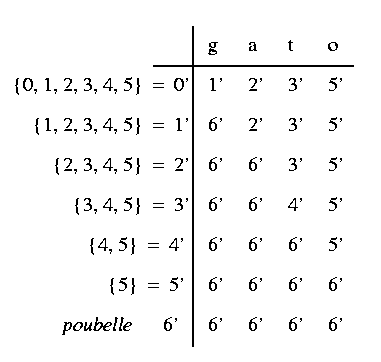
IMPLEMENTATION

Fonction automate_sousmots(). On utilise un array bidimensionnel temp[][] pour travailler temporairement sur la table des transitions.

Le fusionnement est effectué au moyen de deux boucles for emboîtées; après un fusionnement de deux colonnes correspondantes à deux lettres égales, tous les éléments de la colonne égale (colonne qui ne devra plus etre prise en consideration) sont mis au valeur NONVALIDE. Ceci est défini comme MAX_L_MOT+5 pour qu'il soit plus grand à n'importe quel autre numero d'état, étant donnée la relation: numéro d'un etat quelconque <= longueur du mot + 1 <= MAX_L_MOT + 1.
(Pour fixer les idées, on pourrait considerer le valeur de NONVALIDE comme + infini. On rappelle que l'algorithme fait la copie des valeurs les plus petites dans les deux colonnes considérées, donc les colonnes NONVALIDE seront automatiquement écartées.)

Successivement les données vont etre copiés depuis temp sur un vrai modèle d'automate (en excluant les colonnes NONVALIDE); l'etat 0 est marqué comme initial et terminal, et tous les autres, sauf la poubelle, comme terminaux.

CALCUL DES SOUS-MOTS D'UN MOT

Les sous-mots sont toutes les differentes suites de caractéres qu'on peut obtenir d'un mot en lui effaçant de lettres. Leur nombre varie entre n pour un mot constitué de mêmes lettres, jusqu'à n² pour un mot composé de lettres toutes differentes.
Pour le calcul de tous les sous-mots d'un mot donné, j'ai developpé cet algorithme.
Il marche en parcourant l'automate des sous-mots trouvé dans la section précedente.
La complexité est égale a celle de l'algorithme pour la construction de l'automate des sous-mots.

ALGORITHME

J'accouple à chaque sous-mot un nombre entier, que j'appellerai terminus, qui est le numéro de l'etat dans lequel on est parvenu en lisant la derniére lettre du sous-mot.
On commence par écrire la liste de toutes le transitions depuis l'état 0, avec les états d'arrivée correspondants (leur terminus). Ceci sera la liste des sous-mots de longueur 1.
La liste des sous-mots de longueur l est obtenue comme expliqué: pour chaque sous-mot de longueur l-1 dans la liste, on va suivre toutes le transitions depuis son terminus qui mènent à un état terminal (Dans ce genre d'automate, tous les états sont terminaux sauf l'état poubelle, donc il suffit de vérifier que l'état d'arrivée ne soit pas la poubelle). Pour chaque transition, on va écrire à la fin de la liste le sous-mot avec l'étiquette de la transition ajoutée à la fin (et aussi le nouveau terminus relatif à l'etiquette): on obtient un sous-mot de longueur l.
A la fin on obtient une liste complète des sous-mots, ordonnée par la longueur des sous-mots, et ordonnée alphabétiquement par groupe de sous-mots de la même longueur.

IMPLEMENTATION

Elle est réalisée dans la fonction sousmots(). J'ai implémenté l'algorithme d'une facon itérative, mais il se preterait aussi bien à un développement récursif.

Pour mémoriser la suite de sous-mots on utilise deux arrays de struct liste_sousmots; chaque struct contient un array de caractéres sousmot, un entier terminus et un autre entier unique qui ne sera pas utilisé pour l'instant. Une liste (liste_lecture) sera utilisé pour la lecture et une autre (liste_ecriture) pour l'écriture des sous-mots de longueur immédiatement supérieure. Chaque liste contient à la fois un groupe de sous-mots de même longueur.
S'il n'existe pas une liste de lecture, la fonction écrit dans la liste d'écriture les sous-mots de longueur 1. Sinon, pour chaque mot, et pour chaque transition de ce mot, la fonction copie au moyen de strcpy() la liste de lecture dans la liste d'écriture, trouve avec strlen() la position suffix de la derniére lettre du mot et ajoute dans la position suivante l'etiquette de la transition.

La liste complete des sous-mots est obtenu par la fonction tous_les_sousmots(). Elle appelle sousmots(), écrit sur l'écran ou sur fichier la liste d'écriture et ensuite copie la liste d'écriture sur la liste de lecture pour l'itération suivante de l'algorithme. La fonction sousmots() sera appelée n fois, avec n égal à la longueur du mot.
init_liste() sert à initialiser les listes de sous-mots.

CALCUL D'UN PLUS COURT SOUS-MOT QUI SÉPARE DEUX MOTS

Cette partie a le but de trouver une plus petite sous-séquence qui distingue mot 1 de mot 2, c'est-à-dire une séquence qui est sous-mot d'un mot et pas de l'autre.

ALGORITHME

L'idée à la base est de trouver les sous-mots du mot 1 et les sous-mots du mot 2, et successivement les confronter.
La complexité est égale à celle de l'algorithme précedent.

D'abord on vérifiera que les deux mots ne soient pas égaux.
Cette suite d'opérations est à effectuer pour l allant de 1 jusqu'à la longueur du mot le plus long (pour le cas où les mots ne soient pas de la même longueur, on se rappellera que l'ensemble de sous-mots de longueur l d'un mot de longueur k, si l>k, est l'ensemble vide):
- Écrire dans liste 1 tous les sous-mots de longueur l du mot 1;
- Écrire dans liste 2 tous les sous-mots de longueur l du mot 2;
- Pour chaque mot de la liste 1, s'il est aussi dans liste 2, l'effacer des deux listes;
- La liste 1 contient maintenant tous les mots de longueur l qui sont sous-mots de mot 1 et pas de mot 2, tandis que la liste 2 contient tous les mots de longueur l qui sont sous-mots de mot 2 mais pas de mot 1. L'union de deux listes nous donnera la liste des sous-séquences qui distinguent les deux mots. Si cette liste est vide, on répète l'algorithme pour l'itération l+1.

IMPLÉMENTATION

Elle est faite dans la fonction distingue(). Elle utilise les fonctions, écrites dans les sections précedents, qui engendrent la liste des sous-mots.
Apres avoir trouvé les sous-mots d'une certaine longueur l pour mot 1 et mot 2, on les confronte entre les deux listes. On confronte chaque mot de la liste 1 avec tous les mots de la liste 2. On donne à la variable liste_ecr2[x].unique la valeur FALSE si liste_ecr2[x].sousmot est un sousmot commun. La variable locale unique est TRUE pour chaque sousmot de la liste 1 qui n'est pas aussi dans la liste 2, et qui peut donc être affiché. Ensuite on affiche tous les mots de la liste 2 qui ont liste_ecr2[].unique égal à TRUE.
La variable separateurs est le flag qui, si TRUE, indique qu'on a trouvé des sous-mots qui distinguent mot 1 de mot 2. Sinon, on répéte l'algorithme pour les sous-mots de longueur l+1.
A la fin, la liste obtenue est en ordre alphabétique pour chaque groupe de mots qui sont sous-mots d'un mot et pas de l'autre.

JEU D'EXECUTION

Ci-dessous est montré un exemple d'execution du programme.

ken : ~/algo > sousmot

----------------------------------------------------------------------
Projet d'Algorithmique: Outil de Recherche de Sousmots

Licence Informatique
Universite de Marne la Vallee (FRANCE)

       Ce programme est libre et vous etes encourage' a' le redistribuer
             sous les conditions du Licence Publique Generale GNU.
     ----------------------------------------------------------------------

sousmot -help pour les instructions sur l'usage en ligne de commande

1) Examiner un automate
2) Tester l'equivalence de deux AFD complets
3) Creer l'AFD complet des sousmots d'un mot
4) Lister les sousmots d'un mot
5) Calculer les sousmots qui distinguent deux mots

X) Sortie

Operation: 1

Nom du fichier: automate1

AUTOMATE A' 4 ETATS

Etat 0 (Initial) : --a--> 1     --b--> 1
Etat 1           : --a--> 2     --b--> 1
Etat 2 (Terminal): --a--> 3     --b--> 1
Etat 3           : --a--> 3     --b--> 3

----------------------------------------------------------------------
Projet d'Algorithmique: Outil de Recherche de Sousmots

Licence Informatique
Universite de Marne la Vallee (FRANCE)

sousmot -help pour les instructions sur l'usage en ligne de commande

X) Sortie

Operation: 1

Nom du fichier: automate2

AUTOMATE A' 6 ETATS

Etat 0 (Initial) : --a--> 1     --b--> 2
Etat 1           : --a--> 3     --b--> 1
Etat 2           : --a--> 3     --b--> 4
Etat 3 (Terminal): --a--> 5     --b--> 4
Etat 4           : --a--> 3     --b--> 4
Etat 5           : --a--> 5     --b--> 5

----------------------------------------------------------------------
Projet d'Algorithmique: Outil de Recherche de Sousmots

Licence Informatique
Universite de Marne la Vallee (FRANCE)

sousmot -help pour les instructions sur l'usage en ligne de commande

X) Sortie

Operation: 2

Nom du premier fichier: automate1
Nom du deuxieme fichier: automate2

Les deux automates reconnaissent le meme langage

----------------------------------------------------------------------
Projet d'Algorithmique: Outil de Recherche de Sousmots

Licence Informatique
Universite de Marne la Vallee (FRANCE)

sousmot -help pour les instructions sur l'usage en ligne de commande

X) Sortie

Operation: 3

Mot: gatto
Affichage a' l'ecran ou ecriture sur fichier (e/f): e

AUTOMATE A' 7 ETATS

Etat 0 (InitTerm): --a--> 2     --g--> 1     --o--> 5     --t--> 3
Etat 1 (Terminal): --a--> 2     --g--> 6     --o--> 5     --t--> 3
Etat 2 (Terminal): --a--> 6     --g--> 6     --o--> 5     --t--> 3
Etat 3 (Terminal): --a--> 6     --g--> 6     --o--> 5     --t--> 4
Etat 4 (Terminal): --a--> 6     --g--> 6     --o--> 5     --t--> 6
Etat 5 (Terminal): --a--> 6     --g--> 6     --o--> 6     --t--> 6
Etat 6           : --a--> 6     --g--> 6     --o--> 6     --t--> 6

----------------------------------------------------------------------
Projet d'Algorithmique: Outil de Recherche de Sousmots

Licence Informatique
Universite de Marne la Vallee (FRANCE)

sousmot -help pour les instructions sur l'usage en ligne de commande

X) Sortie

Operation: 4

Mot: gatto
Affichage a' l'ecran ou ecriture sur fichier (e/f): e

a
g
o
t
ao
at
ga
go
gt
to
tt
ato
att
gao
gat
gto
gtt
tto
atto
gato
gatt
gtto
gatto

----------------------------------------------------------------------
Projet d'Algorithmique: Outil de Recherche de Sousmots

Licence Informatique
Universite de Marne la Vallee (FRANCE)

sousmot -help pour les instructions sur l'usage en ligne de commande

X) Sortie

Operation: 5

Premier mot: abracadabra
Deuxieme mot: badraca
Affichage a' l'ecran ou ecriture sur fichier (e/f): e

ab
bb
cb
cd
cr
db
rb
rd
rr
dc

----------------------------------------------------------------------
Projet d'Algorithmique: Outil de Recherche de Sousmots

Licence Informatique
Universite de Marne la Vallee (FRANCE)

sousmot -help pour les instructions sur l'usage en ligne de commande

X) Sortie

Operation: x

ken : ~/algo > sousmot -h

NOM
sousmot - outil de recherche de sousmots

DESCRIPTION
Projet d'Algorithmique - Licence Informatique, UMLV (FRANCE)
Copyright (C) 2000 Daniele Raffo <draffo@ken.univ-mlv.fr>

SYNOPSIS
     sousmot [ -x fichier ] | [ -s mot [ reference ]] |
          [ -e fichier1 fichier2 ] | [ -m mot1 mot2 [ reference ]] |
          [ -h ]

OPTIONS
Les options suivantes sont supportees:

-x Affiche sur stdout l'automate decrit sur fichier.

     -s             Affiche sur stdout la liste des sousmots du mot.
                    Si defini, la liste sera place' dans le fichier
                    reference.

     -e             Teste l'equivalence des deux automates decrits
                    dans fichier1 et fichier2. Le code de retour est
                    0 pour deux automates equivalents et 1 pour deux
                    automates non equivalents.

     -m             Affiche sur stdout la liste des plus petits
                    sousmots qui separent mot1 et mot2. Si defini, la
                    liste sera place' dans le fichier reference.

-h Montre cette aide.

Sans parametres, le programme sera lance' en mode interactive.

ken : ~/algo >