Chapter 7
Timestamps

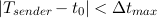
As already said, a common problem in distributed systems is that, even assuming a digest or signature is checked (therefore ensuring integrity or authentication of the source of a message), replay of previously transmitted messages is possible by an intruder. This is the aforementioned replay attack, which may easily corrupt the route cache and therefore discompose the correct functioning of the network.

Timestamps are a commonly used means to prevent replay attacks (as in Kerberos [145]), and are indeed necessary [37, 33]. The idea is to device a proof of freshness, such that older pieces of information can be detected and rejected. Further timestamp methods have been discussed by Gong [56]. When a timestamp is not sufficient, the goal is achieved by using a nonce [112], which is a small sequence of randomly generated bits, used only once. The nonce is sent in a challenge as an identifier and must be included in the response.

In OLSR, MSN (Message Sequence Number) and ANSN (Advertised Neighbor Sequence Number) are already used for achieving those goals in the context of allowing the routing protocol to determine which information is more recent. However while these sequence numbers are sufficient for the basic routing protocol functioning, they are not sufficient to provide full security: each are encoded on a 16-bit field, which implies that wraparound happens too frequently to provide efficient protection against malice from an intruder.

Here we describe several timestamp algorithms, providing different levels of security at the expense of different costs. For the purpose of the discussion we use the following terminology:

• a clock is the device, hardware or software, within a node keeping track of the time;
• a timestamp is the value of a clock, recorded in a piece of information (e.g. a message) at the time of generation of the information.

Commonly, the following methods are employed for providing timestamps:

• Real time: a clock expresses time in some natural resolution such as seconds or microseconds;
• Logical time: a clock is incremented each time an event occurs, such as message generation.

Note that these are just different ways to express the same idea of time: the basic property being that time is monotonically increasing, and that upon receiving a message containing a timestamp the receiving node has some idea about the value in the timestamp compared to the value of the clock, i.e. what the timestamp should be. As concerns the second option, the concept of event ordering in a distributed system has been examined by Lamport [93].

For each message being emitted by a node, an unique timestamp T_sender is included. Let t₀ denote the value of the clock in a receiving node around which the timestamp T_sender in a received message is expected to be. Then, a more formal expression of a message being “not too old” may be:

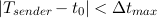(7.1)

where Δt_max is a constant used to limit the timestamp discrepancy while allowing for some small deviation. Thus, the (7.1) provides a simple framework for checking if a received message is original or rather it is a replay of a previous message.

The replay check in the (7.1) can be complemented by maintaining a Signature Table, in order to also prevent replays within a small time-scale i.e. replays within a delay less than Δt_max. The Signature Table contains the signatures (or the digests) of the most recently received messages, for a duration greater or equal to Δt_max. If the signature of a received message is already in the Signature Table, it is ignored since the message has already been received and processed. This is similar to the Duplicate Set in OLSR, which ensures that TC messages are processed and forwarded once. Indeed, the functionalities of both the Signature Table and the OLSR Duplicate Set could be merged.

The way in which timestamps are generated is not necessarily obvious, as they assume either synchronous real-time timestamps, non-volatile timestamps, or they implicitly require a challenge-response protocol.

It should be noted that non-synchronization leaves the door open to clock attacks. If the sender’s clock is ahead of that of a receiving node, an attacker may suppress the postdated message and replay it later, when the timestamp in the message becomes valid according to the receiver’s clock. Re-synchronization of the sender’s faulty clock does not parry this suppress-replay attack [55].

In the following we present different methods concerning the use of timestamps. These methods introduce different levels of complexity, cost, and security tradeoffs; they can also be used in combination, in order to provide greater resilience.

7.1 No timestamps

If no replay protection is desired, nodes may just set the timestamp to be 0 when generating messages, and not check the timestamps upon receiving.

7.2 Real-time timestamps

A conceptually simple way to generate timestamps, although not the easiest one to implement, is to use a real time clock in each node, assuming some kind of synchronization. This solution can be achieved by having a safe source of time in each node that is sufficiently precise and with sufficiently little drift. This could be in form of a quartz clock, an atomic clock, or access to the time as obtained by a GPS device.

The criterion for accepting a message is indeed simply, as in Formula 7.1, ∣T_sender - T∣ < Δt_max, where T is the value of the clock on the receiving node.

The source of time for timestamp generation can often be a quartz clock, or similar equipment, embedded in the node’s hardware. The main issue when using an internal source of time is the precision of the clock. In most computer equipment, piezoelectric quartz oscillators are used to keep track of the time; in personal computers, it is the so-called BIOS clock. The precision of these clocks is nonetheless limited causing a drift, in absolute terms, in the order of magnitude of one second per day. The drift is due to two factors: the lack of precision of the quartz, assumed to oscillate at a certain determined frequency different from the real frequency, and variations in the real frequency due to temperature, aging, vibration-induced noise, and other factors [155].

In order to assess the frequency needed for a possible resynchronization, we conducted experiments [4] with the routers used in the OLSR signature implementation described in Chapter 5. During the experiment, four routers broadcasted their BIOS clock periodically on an Ethernet network. A machine recorded the arrival times of the different broadcasts of the clocks, along with their advertised time value.

All clocks were synchronized at the beginning of the experiment. One of the routers was used as a reference, and the difference between the values of the clocks was recorded and plotted as a function. The resulting maximum clock drift is around 1 sec/day (Figure 7.1), quite comparable with expected values. However, the resulting plotted functions are mostly linear, confirming that the main factor in clock drift is the incorrect calibration of the real frequency of the quartz. By using linear regression on the values found, the linear component of drift between one router and the reference router was removed. In practice such corrections could be performed by making precise time difference measurements at two separate points of time. As a result, the precision is much better and around 30 msec/day (Figure 7.2). Nonetheless, the time functions of some routers were irregular; by comparing the drift estimates based on measurements between different points of time, to the drift estimates based on measurements between the points of time with the greatest discrepancy, the drift is found to be about 0.2 sec/day. The equivalent necessary synchronization intervals for drift correction, for a drift of maximum 15 seconds, are therefore 500 days in the average case, and 75 days in the worst case.

7.3 Non-volatile timestamps

A way to provide weak timestamps is to have the clock of each node of the network maintained in non-volatile memory, initialized the first time a node’s signature key is used after generation.

The value of this clock is then used as timestamp in each message signed, after which the value is incremented. While the sender maintains the clock in non-volatile memory, the receivers maintain a table containing the maximal timestamps received from all nodes in the network.

In the receiver node R, the algorithm for processing a message from sender S with timestamp T_S is the following:

1. R keeps the value of T_S^R, the highest timestamp from S ever received, in non-volatile memory;
2. if R has not received any value from S, R considers the highest timestamp received from S to be T_S^R ← 0;
3. if T_S > T_S^R -D then the message is accepted, otherwise it is rejected and not processed further. D is some fixed (small) constant to allow for out of order reception of messages. D must be tuned accordingly to the specifications of the ad hoc network;
4. T_S^R is updated: T_S,new^R ← max(T_S,T_S^R).

These are security-wise weaker timestamps, since if communication between the sender and the receiver is broken for some time, then the latter goes out of sync and all the messages from the sender can be replayed to the receiver. This is especially true if the sender and the receiver are in different, non-connected, networks. The advantage is that as soon as the receiver and the sender are able to communicate with each other, only limited replay is possible. This replay can further be suppressed with the Signature Table, described previously.

In OLSR, non-neighbor nodes may never exchange messages, because nodes which are not selected as MPR by any other nodes exchange messages only with their neighbor nodes. In this case, the timestamps would never be updated. Therefore it would be necessary that each node periodically broadcasts at least an empty message in order to provide synchronization.

Note that a variant using a local “wall clock” time instead of incremented timestamps is possible, and could allow more stringent checks, although the algorithm still remains vulnerable.

7.4 Clock synchronization

With respect to clock synchronization, the chicken-and-egg dilemma arises [56]: timestamps are used for authentication, but secure clock synchronization itself requires authentication. This circular dependency is overcome by performing authentication and clock synchronization operations at the same instant. However the main problem with secure clock synchronization in an ad hoc network is that many algorithms require a fixed percentage of non-compromised nodes in order to operate. It could be argued that, since in an ad hoc network an intruding node can impersonate as many fictional nodes as it wishes [39], under the limitation that these fictional nodes have keys known to the network, a guaranteed fraction of non-compromised nodes is unobtainable. Even a clock synchronization algorithm such as that proposed by Dolev et al. [37], which does not require any such fraction of correct nodes to run properly, provenly cannot bound the necessary delay of synchronization when a new node wishes to participate in the network for the first time. This is quite problematic in a wireless ad hoc network, since nodes are expected to be able to leave and join at any time.

7.4.1 Timestamp exchange protocol

This part describes a timestamp exchange protocol that can be applied to OLSR. It essentially mixes a distributed challenge-response protocol with timestamp information. This protocol is a variation over the Needham-Schroeder public key protocol [112], albeit with a superset of the information (and includes, for instance, the necessary correction of the protocol proposed by Lowe [99]), using signatures instead of encryption, and using timestamps instead of nonces.

The assumption for the protocol is that each node X keeps a clock T_X, whose value is used in the timestamp fields of generated messages. The clock increases monotonically with each message sent, and with wall clock. At a given wall clock time t, the clock in the node A is denoted T_A(t). The clock T_A is also used as a nonce, and thus should be initialized, fully or in part, with random values.

A simplified version of the protocol is given first, illustrating the gist of the protocol limited to two nodes A and B.

1. At t₀, A → B : {A,T_A(t₀)}_A;
2. At t₁ > t₀, B has already received the previous message and sends its message: B → A : {B,T_B(t₁),A,T_A(t₀)}_B;
3. At t₂ > t₁, A has received the previous message and sends its message: A → B : {A,T_A(t₂),B,T_B(t₁)}_A.

The idea is that at t₂ (step 3) A had received the message sent in step 2, and thus observed that a recent version of its timestamp T_A(t₀) was included in a message, authenticated to be from B. Therefore A can safely assume that T_B(t₁) is a recent value of the timestamp from B, posterior to t₀. This relies on A properly generating initial values of clock T_A i.e. not (or with low probability) repeating values over the time.

Likewise, upon receiving the message sent from A to B in step 3, B concludes, like A, that it has now a recent authenticated value of T_A. After those steps are complete, A and B both have knowledge about relatively recent values of each others respective timestamps, which are not (or with very low probability) the result of replays. In this case we say that the handshake is completed.

A detailed parallel version of the algorithm now is given. It is “parallel” in the sense that the same message, sent by a node A to perform the previously illustrated handshake, is sent this time to several nodes (ideally all) in the network, rather than to an individual node B. Also some provisions are taken for being able to practically perform timestamp check, and for switching to new timestamp intervals.

The protocol relies on an unique new kind of message, a Timestamp Exchange message, being flooded periodically by each node. When maximal security is desired, the message should be transmitted by pure flooding to the network instead of using the MPR forwarding optimization.

We assumed that each node keeps a table of the information from the latest Timestamp Exchange message it received from each node. This table is called the Timestamp Table. A node A records the following information for each other node B:

• a boolean H_B^A indicating whether the handshake with B has been completed,
• the timestamp T_B^A from the latest Timestamp Exchange message received by node A from node B (in case the handshake is completed), or the list of the latest timestamps T_B,j^*A received (in case the handshake is not completed),
• a set of different timestamp interval tuples for i = 1,…,n_B^A: where E_Bi^A is an expiration time indicating that the tuple should only be used until this time value is reached, when the handshake is completed.

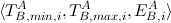
In node A, each timestamp interval tuple of B describes a valid interval for timestamps of B. There are several such timestamp interval tuples for B (several is) in order to allow for timestamp interval changes. Such a change would occur, for instance, when the node decides to regenerate a clock’s value from scratch. The timestamp interval tuples are used with the following timestamp check: in node A, at t, a timestamp T_B from a message from B is valid if and only if an i exists such that T_B,min,i^A ≤ T_B ≤ T_B,max,i^A and t < E_B,i^A.

This timestamp check does not apply to Timestamp Exchange messages themselves, described below.

At node A, given two valid timestamps T_B and T′_B from B, an ordering relation can be established for comparison. Let j and j′ be the indexes such that T_B,min,j^A ≤ T_B ≤ T_B,max,j^A and T_B,min,j′^A ≤ T′_B ≤ T_B,max,j′^A. Then we decide that T_B > T′_B if and only if j > j′ or (j = j′ and T_B > T′_B). This is used for determining which of two messages, to which the timestamps relate, is the most recent.

For protocol completeness, in node A the timestamp T_B^A is said to be orphaned when H_B^A is false or when T_B^A does not pass the timestamp check with any of the timestamp intervals and expiration time 〈T_B,min,i^A,T_B,max,i^A,E_B,i^A〉. This can occur when some (or all) of those intervals expire, usually meaning that communication between node A and node B is broken.

This yields a formal definition of “completion of handshake between A and B”: a handshake is complete for node A when B has a timestamp T_B^A which is not orphaned. Each time H_B^A was true and the timestamp T_B^A becomes orphaned because of timestamp interval, H_B^A is updated as: H_B^A ← false.

The protocol relies on two parts: the generation and the processing of Timestamp Exchange messages.

The algorithm for the generation of the messages is as follows: node A sends periodically a Timestamp Exchange message, containing:

• its current clock T_A^new, which must not be orphaned with respect to the bounds set out in the following item;
• its current timestamp bounds set n_A^new, and for i = 1,…,n_A^new: where D_A,i^new is the maximal duration for which the tuple should be kept;
• the content of its timestamp table, tuples 〈X,T_X^A〉 for each node X from which it has received a timestamp. Note that for each X with which the handshake is not completed there might be several 〈X,T_X,j^*A〉. In this case, once the 〈X,T_X,j^*A〉 has been sent, the tuples are removed;
• the signature of this message.

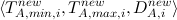
Node A also records the latest timestamp bounds set it has sent:
(T_A,min,i,T_A,max,i).

The algorithm for the processing of the Timestamp Exchange messages for a node A receiving a message from node B is as follows:

1. check for the entry of B (if it exists) in the Timestamp Table to determine if H_B^A was true but the T_B^A has become orphaned. If T_B^A has become orphaned, then H_B^A ← false;
2. if no reported timestamp from A, inside the Timestamp Exchange message, pass the timestamp check in A, or if there is no T_A in the message, then: if no entry for B was recorded, or if H_B^A is false, the timestamp from the message T_B is added to the list of the timestamps T_B,j^*A.

   The idea here is that node B has not provided enough proof of freshness for A to accept the timestamp intervals. However T_B should be kept such that in next message from A it would serve as proof of freshness. All T_B received should be kept since some could constitute invalid replays;

3. otherwise, the handshake is certain to be completed and the timestamp bounds are updated if necessary:
   1. if no value T_B^A was recorded or if H_B^A was false, or if the new timestamp T_B of the message is greater than the latest timestamp recorded T_B^A (with the timestamp comparison rules given previously), then:
      1. T_B^A is updated with the timestamp from the message, the previous list T_B,j^*A is emptied, and T_B^A ← T_B;
      2. the timestamp bounds for B are updated with the values from the Timestamp Exchange message: n_B^A ← n_B, and for i = 1,…,n_B: where t is the wall clock at node A.
   2. H_B^A ← true.

It is expected that the timestamp bound set of a node is limited to an interval (T_A,min¹,T_A,max¹), and only occasionally updated when a new timestamp interval (T_A,min²,T_A,max²) is generated. The transition is typically the following:

1. A advertises the interval (T_A,min¹,T_A,max¹) and generates timestamps in this interval;
2. for some duration, A advertises interval (T_A,min¹,T_A,max¹) and a new interval (T_A,min²,T_A,max²). Node A will still generate timestamps from the first interval, to wait for the new interval to be updated in receiving nodes;
3. for some small duration, A advertises both interval (T_A,min¹,T_A,max¹) and interval (T_A,min²,T_A,max²). A now generates timestamps from the second interval, while it keeps advertising the old interval;
4. A advertises only interval (T_A,min²,T_A,max²).

Note that it is possible to add variations: updating also the timestamp table on reception of messages like HELLOs, introducing some maximum deviation Δt_max from the last received timestamp, or using local wall clock (possibly with a random offset) instead of an incremental counter. It is possible to add optimizations to avoid sending lists of timestamps of the same node before handshake completion, such as sending immediately a Timestamp Exchange message, along with Denial of Service detection with respect to the handshake protocol.