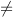 x such that h(x′) = h(x) (second preimage resistance);
x such that h(x′) = h(x) (second preimage resistance);
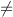 x′,
such that h(x) = h(x′) (collision resistance).
x′,
such that h(x) = h(x′) (collision resistance).A secure system may be defined as a system that does exactly what its designers conceived it for and does not show any unexpected behavior, even when an attacker tries to make the system act differently.
A definition of security is indeed incomplete without specifying against who or what the system is secured. Furthermore, as absolute security is impossible to obtain, a report about the cost/benefit balance must be established.
It must be recalled that enforcing security requires that the defender covers all points of possible attack, as, for the attacker, it is sufficient to focus its efforts on one weak point in order to succeed. Therefore a system is only as secure as its less reliable security point. This is synthesized in the widely known expression: “a chain is as strong as its weakest link”.
When talking about security of a communications network, there are different areas in which this topic applies. The major security goals are defined with the terms which follow; for each goal, the associated attack is identified. The name can describe either the functioning of the attack or its effect.
Other security goals may be more difficult to achieve. Note that attacks can be combined, e.g. the intruder may break into the system in order to prepare a DoS from inside, or may perform eavesdropping with the purpose of later gaining unauthorized access.
Many security countermeasures are achieved by the use of cryptography [139, 13].
Encryption is the process of disguising a message in such a way that it hides its content; the operation consists in transforming the message from plaintext to ciphertext. The inverse process is called decryption.
It is also possible to add a message digest, also called a hashing or digital fingerprint, to the message so that the integrity of the message can be verified.
Signing a message means, instead, to add a sequence of bits (a digital signature) to the message in order to identify its real originator.
These techniques are performed by using a cryptographic algorithm (cipher) and a key, whose format depends on the algorithm used. It is often necessary to apply more than one technique, i.e. a message can be encrypted and then digitally signed.
With respect to the aforementioned security attributes:
Authentication, and subsequent access control, is more complicated to obtain and requires the use of more advanced cryptographic primitives, while service availability is not the concern of cryptography.
It is likely that information that was true at some time in the past may not be true anymore in the present. A common problem is that, even assuming a digest or signature is successfully checked, previously transmitted messages can be sent again by an attacker. That is, an intruder may record a bulk of messages and re-send them some time later; these messages, if they cannot be identified as old (by some definition of “old”), will be accepted as valid because they are properly signed. This is known as replay attack, and may easily disrupt communications. To oppose replay attacks, messages usually embed a piece of time information, called timestamp, describing the time at which the message was generated. The timestamp is included in the computation of the signature. Timestamps are discussed in detail in Chapter 7.
An adversary may exploit possible weaknesses in cryptographic functions. For instance, when relaying a control message with digest from one node to another, an attacker may replace the original message with a forged one which, due to a flaw in the digesting algorithm, has the same digital fingerprint. The adversary discovers these flaws using different techniques e.g. plaintext-chosen or brute-force attacks, depending on the data available to work on. These kinds of codebreaking attacks (cryptanalysis) are aimed against the cryptographic layer, and do not require the disclosure of any key to the attacker. However, when designing security schemes that rely on cryptography, it is usually assumed that cryptographic primitives are robust against these attacks.
Two branches of cryptography exist: symmetric cryptography and asymmetric cryptography. Each is useful to perform different functions.
Symmetric cryptography (also called secret key cryptography, single key cryptography, or one key cryptography) is the most ancient form of cryptography. Symmetric cryptography is based on symmetric key algorithms, i.e. algorithms where the encryption key and the decryption key are the same (or, more broadly, where the encryption key can be computed from the decryption key and vice versa). The sender and the receiver of a message must agree on a secret shared key, which will henceforth be used to encrypt, decrypt, and generate a digest on exchanged messages.
Some of the symmetric algorithms for encryption are: DES with its improvements Triple DES and AES, IDEA, LOKI, Lucifer, Skipjack, Vernam (also known as one-time pad), RC2, and RC4.
To this class of algorithms also belong the ancient substitution and transposition ciphers, like Caesar, Mary Stuart’s, Pigpen, Vigenere, Playfair, and ADFGVX. These ciphers were in use centuries ago, in the pre-computer era, and are not used anymore because they are easy to break by applying cryptanalysis.
Symmetric algorithms make large use of hash functions [106] for digesting. A hash function h maps a bitstring of arbitrary finite length to another bitstring of fixed length n, where n depends on h. The hash function hence outputs a hash value which is a condensed representative image of the bitstring fed in input. Changing just one bit of the input string results in a very different hash value in output; this is known as the avalanche effect.
A hash function h should have the following properties:
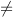 x such that h(x′) = h(x) (second preimage resistance);
x such that h(x′) = h(x) (second preimage resistance);
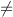 x′,
such that h(x) = h(x′) (collision resistance).
x′,
such that h(x) = h(x′) (collision resistance).Examples of hash functions are MD5 (Message Digest 5) [134] which is the successor of MD4, Snefru, RIPEMD-160, and the class of SHA (Secure Hash Algorithm) functions [113] such as SHA-1 [40] and SHA-256.
Cryptographic literature often references a random oracle [10, 23]. A random oracle is a theoretical model of a “perfect” hash function which returns an answer uniformly selected amongst all possible answers.
A hash function may be used in conjunction with a secret shared key (e.g. by concatenating the key to the hash input) to construct a keyed hash function. In this case, the digest is more often called Message Authentication Code (MAC)1. This is the foundation of the HMAC mechanism [9, 91]. The resulting keyed hash function is called with a name that depends on the hash function used, for instance HMAC-MD5, HMAC-RIPEMD, or HMAC-SHA1.
In asymmetric cryptography (also called public key cryptography), there is a key for encryption (public key) and another key for decryption (private key or secret key). A public and its companion private key compose a key pair; knowing a public key, it is computationally infeasible to calculate the companion private key. A party can leave its public key available to everyone, e.g. by publishing the key in a public directory; its private key needs to be kept undisclosed. All public key exchange may be done over an insecure channel, i.e. a channel that may be subject to eavesdropping. Public key cryptography therefore requires a Public Key Infrastructure (PKI) to authenticate the parties, generate the key pairs, or distribute, update and revoke the public keys.
Public key cryptography was introduced by Diffie and Hellman [35] in 1976
(and developed further by Merkle [107]), but independently discovered some
years earlier by Cocks and Williamson of GCHQ. The Diffie-Hellman key
agreement protocol allows two parties to share a secret key over an insecure
channel.
One of the greatest problems in a PKI is about how to bind a public key with its legitimate owner – that is, how to be sure that a specific public key belongs to a party and not to an impostor, which would then be able to decrypt messages supposedly sent to that party. If two parties, Alice and Bob (we call them so in the tradition of cryptographic literature), want to exchange their public keys, they could do it over the same insecure channel that is used afterward to swap their encrypted messages. However, if an adversary is able to tamper with communications over the channel, it can make the protection unsuccessful. This is a kind of double identity spoofing, called man-in-the-middle attack, in which an adversary stays in the communication channel between two parties and acts with a party as the other party. The parties are deluded that they are talking with each other, while in fact the invisible adversary relays their messages.
The attack is performed as follows. The adversary generates two public/private key pairs {PX,SX},{P′X,S′X}. Alice sends her public key PA to Bob, but the adversary intercepts it, substitutes the legitimate key with its public key PX, and sends PX to Bob. Bob sends his public key PB to Alice, but the adversary intercepts and substitutes it with P′X, which is sent to Alice. As a result, Alice mistakenly believes Bob’s public key to be P′X, and Bob mistakenly believes Alice’s public key to be PX, while both keys are owned by the adversary:
| Alice {PA,SA} |
←- | adversary {P′X,S′X} {PX,SX} |
-→ | Bob {PB,SB} |
From this point on, the adversary intercepts unnoticed any message sent from Alice, decrypts it with S′X, reads it, re-encrypts it with PB, and sends the message to Bob which decrypts it with his private key SB. In the opposite direction, the adversary intercepts any message from Bob, decrypts it with SX, reads it, re-encrypts it with PA, and sends the message to Alice which decrypts it with her private key SA. Therefore, the adversary is able to read any message exchanged between Alice and Bob, while they are unaware of the adversary’s presence and think their communications are kept confidential.
One solution to this problem involves a Trusted Third Party, which must be trusted by everyone. The TTP stores the public key of every participant and guarantees on the owner of each key. Depending on the implementation, the TTP is called Key Distribution Center (KDC) or Certification Authority (CA). A Certification Authority delivers certificates containing the identity of the key’s owner, its public key, the certificate validity dates, and other information; each certificate is signed by the CA, which public key is known a priori by every participant.
For instance, the solution of bestowing a Certification Authority is broadly utilized in the SSL/TLS protocol [148] (on which HTTPS, the secured Internet protocol, is based), IPsec, S/MIME, and others. SSL certificates follow the X.509 standard [50, 63] developed by the International Telecommunication Union - Telecommunication Standardization Sector, and can be delivered by many commercial CAs: RSA Security Inc., VeriSign, ValiCert, and VISA, just to name a few. The public key of each CA is embedded in web browsers and other network applications. Public institutions and government agencies may have their own CAs, too.
However, the existence of a trusted party is a point of fragility of the whole PKI. If the deliver of public keys is done on demand, an adversary could paralyze the whole network by launching a Denial of Service attack against the KDC. Furthermore, by compromising a Certification Authority, the attacker can issue fake certificates for any identity it wishes, to prepare spoofing and man-in-the-middle attacks.
To securely send a message, the sender retrieves the receiver’s public key, encrypts the message, and sends it to the receiver which can decrypt it with its private key.
Examples of asymmetric ciphers for encryption and decryption are RSA (Rivest-Shamir-Adleman) [135, 136], Knapsack, and ElGamal; other ciphers are instances of elliptic curve cryptography (ECC) applied to canonical algorithms, such as ECC ElGamal. ECC is an approach to the public key problem based on the mathematics of elliptic curves.
Asymmetric ciphers for signatures are composed of a private and a public part. To sign a message, the sender uses the private algorithm. The receiver of the message then verifies the signature by applying the public algorithm. For simplicity, it is often said that the sender uses its private key to sign while the receiver verifies the signature with the sender’s public key.
This is the case of RSA, where the sender generates a hash of the message and encrypts it with its private key. The receiver will use the sender’s public key to decrypt the sent hash and check if it matches the recomputed hash. This works because, in a RSA key pair, both the public and private key can be used to encrypt, while the other key is used to decrypt.
Examples of asymmetric schemes to generate digital signatures are Fiat-Shamir, Ong-Schnorr-Shamir, and DSS (Digital Signature Standard) [114] which includes DSA (Digital Signature Algorithm); ECC schemes such as ECNR (Elliptic Curve Nyberg-Reuppel) and ECDSA; and, again, RSA and ElGamal.
Symmetric and asymmetric cryptography has both weak and strong points. Arguments in favor of symmetric cryptography are:
On the other hand, asymmetric cryptography is superior in some perspectives:
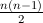 symmetric keys. Furthermore, if these keys are committed to a Trusted
Third Party, this TTP must be unconditionally trusted as it is
theoretically able to encrypt and decrypt any message from or to any
party. Using asymmetric cryptography, the number of keys to manage
is just O(n). Only the public keys are entrusted to the TTP, which
therefore needs only to be conditionally trusted.
symmetric keys. Furthermore, if these keys are committed to a Trusted
Third Party, this TTP must be unconditionally trusted as it is
theoretically able to encrypt and decrypt any message from or to any
party. Using asymmetric cryptography, the number of keys to manage
is just O(n). Only the public keys are entrusted to the TTP, which
therefore needs only to be conditionally trusted.
In summary, symmetric cryptography is efficient for encryption and data
integrity tests, whilst asymmetric cryptography is cogent to generate
digital signatures and manage keys. A cleverly designed cryptographic
application would exploit the advantages of both schemes: a public key
exchange could be used to establish a symmetric key between two parties,
while further communications would be encrypted using the symmetric
key.
The next chapter provides a classification of the attacks against the routing
layer. In Chapter 4 and 5, we show how cryptography can be used to thwart
these attacks and enforce security. Chapter 6 offers a dissertation on the
available ciphers, considering the requirements and limitations of an ad hoc
environment.